前のページでは、電子工作を5000円で始める工具・部品セットを紹介しました。 ここでは、電子工作を始めるにあたり、用意したほうがいい電源についてのことや、常用する5Vの電源をUSBアダプターで作ることなどを紹介しています。
このHPはほとんど5Vの直流電源を使います
電子工作をやっていくためには、安定した電圧の電源が必要で、このHPでは、5V電源を主に使っています。
USB用でも使われる5Vの電源は、このHPで取り扱うIC類にも適しているので、余っていて使わない充電器を加工して使うといいでしょう。（文章の後半で紹介）
「乾電池」を使ってもいいのですが、4個を直列にすると6.4V以上になってしまいますし、使っていると、電圧低下が起こり、電圧が一定にならなくて使いづらいので、このHPでは、USBの5Vの定電圧電源を使っていきます。
最近では、USBポートのついているコンセントなども増えていますし、USBポート付きの100V用コンセントでもOKで、この場合は、接続するコード（USBコード）を加工して使うといいでしょう。
ただし、パソコンなどの機器のUSBポートを使うと、トラブルが起きた場合に困りますので、ここでは、工作の一環で、家庭にあまっている5V充電器のコードの先端を細工して、ブレッドボード用の専用電源を作ります。参考になれば自作してください。
もちろん、可変できる市販の電源があれば、遊べる範囲が広がりますので、ここでは、その他の電源についても紹介しています。
スマホ充電器のコード部分を細工しています
ちなみに、このアダプターは「5V 1A」です。0.5～2Aでもほとんど問題はありまん。
加工後の5V電源
ここでは、ブレッドボードにさして給電できるようにピンを加工しましたが、下のように、虫ピンや細いゼムピンを代用してもいいですし、ワニ口クリップをつけるのもいいでしょう。
PR工作は簡単ですので、自分流でやってみてください。USBコードの線は非常に細いので、下のように、熱収縮チューブで補強しておくといいでしょう。
ゼムピンを代用した先端
ワニ口クリップや細い電線などは、家庭にあるものをつかえばいいですし、100円ショップやホームセンターでも販売されています。
加工方法は、ジャック側の先端を切断して、コードの皮をはいで、4本の線をテスターで電圧をはかり、電圧のかかっている2本の線に、差し込み用のピンなどをはんだ付けするだけです。
このUSBコードの場合は「赤・黒・緑・シロ」の4本があって、「赤と黒」の2本から5Vの電圧が出ています。 他の2本（緑・シロ）は使いませんので殺しておきます。
細い線なので、熱収縮チューブやビニールテープなどで補強ておきましょう。
テスターでその電圧を測ると、4.94Vになっていて、電圧は、安定しています。
【参考】このHPでは、FETやオペアンプの記事に、電源を2つ（または正負の電源）使う記事が出てきます。 家庭に5Vのアダプターが余っておれば、そのときに使いますので、このような充電用アダプターや付属の線は、捨てずに保管しておくといいでしょう。
PR電子工作で使う電源について
自作しなくても、その他でも直流の「安定化電源」であればOKです。
以前によく使われていたAC-DCアダプターは電圧を下げて直流化しただけのものが多いので、これらは写真にあるように、いい加減な電圧になっているので、このままでは電子工作には使いにくいです。
試しに電圧を測って見ると、下のように、呼び電圧に比べて、無負荷ではびっくりするほど高い電圧になっています。
私達がこれをこのまま電子工作に使おうとすると、これではちょっと困りますので、電子工作の電源として使う場合は、定電圧のアダプターを使うようにしましょう。
（参考）このページの後のほうに、三端子レギュレータを使って、安定化した電源を作る記事があります。 参考にしていただくといいのですが、ほとんどの電子機器は、三端子レギュレータなどを使って、機器内部で安定化しているものが多いので、これらの非定電圧アダプターは、少し高めの電圧になっているものが多いです。
持っていると便利なアダプター（電源）の例
私は、下の写真のような、市販品のアダプター（3～12V用）や、可変の電源なども併用しています。
この製品本体後ろのスイッチで6段階の電圧を切り替えるようになっており、電圧も安定していて、1Aまで使用できるうえに、いろいろなDCジャックを付け替えるようになっています。
ブレッドボード用でないので、ピン付きのものや、ワニ口クリップ付きのコード（電線）を作っておけば、いろいろな場面で使うことができます。（「工作」して楽しんでみてください）
アマゾンの記事を見ると、1500円程度から各種が販売されています。 参考に。
安価でいろんな電圧に対応のACアダプター（Amazonのページ）
大きな電流で使いたいときに・・・
1Aの電流容量でもこのHPの電子工作では結構大きな電流ですが、もっと大きな電流で使いたい場合もでてくるでしょうから、使わなくなったアダプターなどを捨てないで、残しておくようにしましょう。（こうして、どんどん、ガラクタが溜まっていくのですが・・・）
余談ですが、電気を使うときには、常に、「大電流＝発熱」と言うことを考えるようにしておいてください。
電子工作は安全第一ですから、常に「熱」を意識しておく必要があります。 電流をたくさん流して使うと、熱がでるので、熱に対する配慮や注意を意識しましょう。
PR便利な電圧可変電源
電子工作には、お金をかけると、際限がありませんが、今後も、色々な実験を楽しみたい方は、このような可変の電源を購入しておくと便利です。
私が購入したこの安定化電源（STP3005D）は最も安いランクの機種で、5千円ちょっとの価格です。 いろいろな場面で使うことができて、結構便利です。
仕様は5A 0～30Vで、電圧を可変して使う使い方がほとんどですが、電流を制限して使うこともできます。 例えば、電流を100ｍA以下で使う場合などでは便利です。（ただし、設定、表示は0.1A単位なので、おおざっぱですが・・・）
Amazonの安定化電源のページ
このHP記事では、交流はほとんど使いませんが・・・
これは、6-12V（実効値）の交流トランス（TOYOZUMI HT-1205 ： 1000円程度）です。
私は、ブリッジダイオードを使った整流や、LEDの交流点灯などの実験のために、これを購入しましたが、このHPでは、交流は、ほとんど使わないものの、実験好きの方は、このような交流トランスがあると、いろいろなことに使えて便利でしょう。
「負電源」の話
オペアンプを使おうとすると、「正・負電源」を使う場合がでてきます。 このHPでは、基本的な内容だけですので、今のところは、両電源ではなく、単電源で動作するオペアンプを使用しており、両電源は使いませんが、こちらのオペアンプのページで取り上げています。
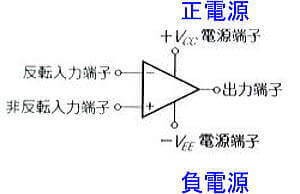
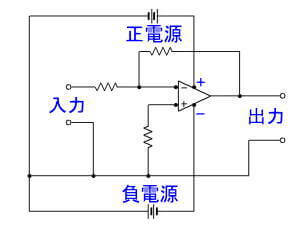
一般的には「電源部分は省略する」ので、負電源がどんなものかは分かりにくいのですが、両電源で使うオペアンプは、上右図のように、正と負の電圧を加える必要があります。
こちらのJFET（ジャンクション電界効果トランジスタ）の記事でも負電源が出てきます。
正・負電源用の3端子レギュレータを使っての製作もいいのですが、このHPでは、USBアダプターを2つ用意して間に合わせています。 興味ある方は、ぜひ電源製作にトライしてください。
使用中の発熱については注意しましょう
リチウムイオン電池が充電中に発熱・発火するニュースを目にすることがありますが、電気を使う限りは発熱による問題は意外に多いものです。
電子工作をしているときにも、異常な発熱には、常に気を使っている必要があります。
私が自作した三端子レギュレータを使った電源で実際に起きた問題の例ですが、ここで使った L78L05ACZ は、100mA用の小さい容量のもので、上の写真のように、放熱板がない構造で、これに、規格値の半分の5V・50mA 程度の電流を流して使用したのですが、手でさわれないくらいの高温度（約50℃以上）になりました。
データシートをみると、100℃程度になっても、出力が落ちない仕様になっていますが、50℃でも手でさわれないくらいの温度ですから、この部品が壊れなくても、周りの電子部品の部品配置や放熱には常に配慮する必要があることを頭に入れておく必要があります。 ともかく、熱・発熱には常に気をつけておかないといけないことを頭に入れておいてくださいね。
次のページでは、回路図、オームの法則、対抗の合成などの内容取り上げています。 知っていると便利ですが、知らないと前に進めないというものでもありませんが、忘れていればサラッと読んでいただくといいでしょう。
（関連記事）
→次のページ ： 三端子レギュレータを使った電源の製作・その他
PR
