バイポーラトランジスタのダーリントン接続
ダーリントン接続とは、2つ以上のトランジスタを使って、高い増幅率を得る回路で、一般のバイポーラトランジスタ(例えば2SC1815など)を連結するだけの、簡単な回路です。
これを使うことで、非常に高い増幅ができるのが最大の特徴です。
近年はオペアンプがよく使われています。 パイポーラ型のオペアンプは、内部でダーリントン結合回路を使って、高い増幅率が得られるようになっていますし、ダーリントントランジスタと呼ばれる、内部でダーリントン接続回路を持つ高増幅度を持つトランジスタもあります。
ここでは、バイポーラトランジスタ2SC1815 を使って、ダーリントン接続回路を組んで、高い増幅率を得る方法を実際に試してみましょう。
通常のトランジスタでは、例えば電流増幅率は50~300程度のものが多いのですが、このダーリントン接続回路を使えば、トランジスタの増幅率の掛け算 (例えば、増幅率100のものを2つ用いれば、10000倍というように)で、とてつもなくすごい増幅ができます。
マイクから拾った微小電流を増幅する場合などでは、オペアンプを使うことが多いのですが、このダーリントン結合を使うことでも、同じようなことができます。 難しい内容ではないので、ダーリントン接続について見ていきましょう。
またここでは、電子工作を楽しもうとしている方に応用して使っていただきたいので、いろんな余分なことを付け加えて書いていますし、計算もあるのですが、気にしないで、ヒントになりそうなところだけをピックアップしていただくといいでしょう。
基本のダーリントン回路
ここでは、下の回路の、NPNのバイポーラトランジスタを使ったエミッタ接地の回路だけを見ていきますが、原理を理解するのは、これが一番わかりやすいと思います。
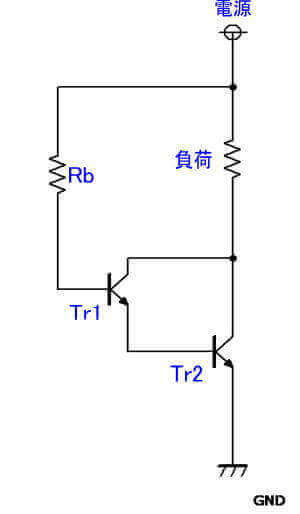
このように、トランジスタを2つつないだものをダーリントン接続といいます。
今までと同じように、2SC1815を使って、5Vの定電圧電源を使って、この回路について、いろいろなことを見ていきましょう。
もちろん、他のNPNトランジスタも同様に使えますので、手持ちのものを使って試してやってみてください。
前のページで説明しているように、2SC1815 に限らず、NPNトランジスタで似たような電力増幅用トランジスタが手元にあれば、同じようにそれらを使っても問題ありません。
前のページで使ったときの2SC1815の電流増幅率は、ほぼ100でしたので、2SC1815の電力増幅率が100であれば、2つのトランジスタをダーリントン接続して使うと、この回路では、100x100=10000倍という増幅率になるというのです。
しかしもちろん、これは、理論上の値で、実際には、ベース電圧、ベース電流、コレクタ電流、温度など、トランジスタ個々の特性や条件によって、その時の増幅率が変わるでしょうし、使うトランジスタの増幅率が 100 なのかどうかは測定してみないとわからないのですが、それはともかく、2つのトランジスタを使ってこの回路にすると、増幅率は 足し算するのではなく「掛け算する」・・・という増幅になる理屈ですので、すごい増幅率が得られるのです。
このようなことを、知っているのと知らないのとでは、「遊び」の内容が変わってくるでしょう。
ここからは、頭の中で考えたことをブレッドボードに組んで、電流値などを測定していくのですが、ぜひ自分でやってみて、実際に確認していただきたいと思います。
回路の数値を決めて、測定して確認してみます
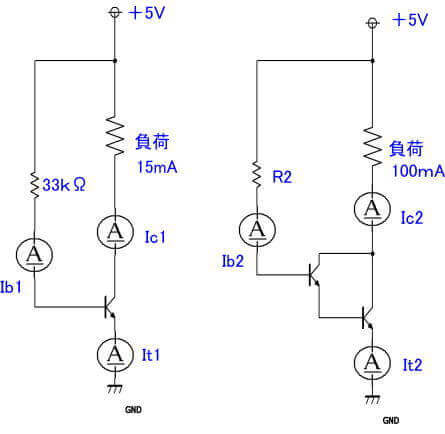
回路を簡単にしてありますが、左がこれまでのLEDの点灯で使ったトランジスタの増幅回路で、右がこれから考えようとしているダーリントン回路です。
ベース電流を決める抵抗の計算
今までのおさらいをしながら、ダーリントン回路の上図の 「R2」 をきめることを考えていきます。 一つずつ考えて行きます。
左側はLEDに15mAの電流が流れるようにするために、前のページでは、計算しやすいように、下の3つから、33kΩの抵抗値を決めました。
①コレクタ電流Ic=ベース電流Ibx電流増幅率h
②コレクタ電流Ic=エミッタ電流Ie
③エミッタベース間電圧Vbe=0.7V ・・・でした。
トランジスタ2SC1815の電流増幅率を100 として、オームの法則から、Ib1に流す電流は、0.015/100=150μA で、③で、トランジスタの電圧降下は0.7Vから、求めたい抵抗値は R=E/I から、 (5-0.7)/0.00015=28.7kΩ となり、市販されている近い抵抗器を探すと 33kΩ ・・・ が近いということでそれが決まりましたね。(前ページでやった復習です)
これと同様に、ダーリントン回路について考えると、電流増幅率は100x100の10000なので、1つ目のトランジスタに流すベース電流Ib2は、 0.1/10000=10μA で、さらに、トランジスタが2つなので、0.7x2の電圧降下があるとして、オームの法則から、 (5-1.4)/0.00001=514kΩ と計算できます。
市販のものでそれに近い抵抗器は510kΩがありますので、R2は510kΩを使います。
次に負荷についてどうするか・・・ですが
負荷をつないだときに、100mAの電流が流れるとして、「抵抗器」を代用して、回路を組みたいのですが、その抵抗値はいくらにすればいいのでしょうか?
これも、オームの法則で計算できますね。
R=E/I から、100mA流して5Vの電圧降下があるのですから、5/0.1=50Ω の抵抗をつければいいということになります。
このときの消費電力は、P=IE から 0.1x5=0.5(W)なので、安全のために、その3倍の1.5W以上のワット数の抵抗器を使う必要があります。
しかし、短時間に電流を確認すればいいので、適切な使い方ではないのですが、200Ω(1/8W)の抵抗器4本を並列にして、間に合せですが、1/8x4=0.5Wで使いましたが、あまりおすすめしないやり方ですが、注意しながら実験します。

確認用の回路を組んで、コレクタ電流、ベース電流などを測定すると、下図のようになりました。

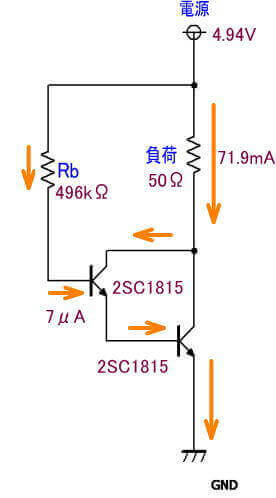
この図のように、7μAを2SC1815のベースに流すと、71.9mAのコレクタ電流を流れました。
これを単純計算すると、71.9/0.007=10271倍の増幅率になっていることがわかります。
ダーリントン結合のすごいところが確認できました。
応用例として、LEDを点灯させてみましょう
電流測定の実験をするだけなら、このような抵抗器の負荷でもいいのですが、やはり、目に見えてわかるのが楽しそうなので、やはりここでは、LEDを使って何かしてみましょう。
ここでは、遊び心から、手持ちのLEDで、「順電圧3.5-4.0V RGB(FAST)」という7色に点滅する派手なLEDがありますので、それを使って、上のおさらいをしながら、実験をしてみます。
ボリュームでLEDの明るさを変えてみましょう
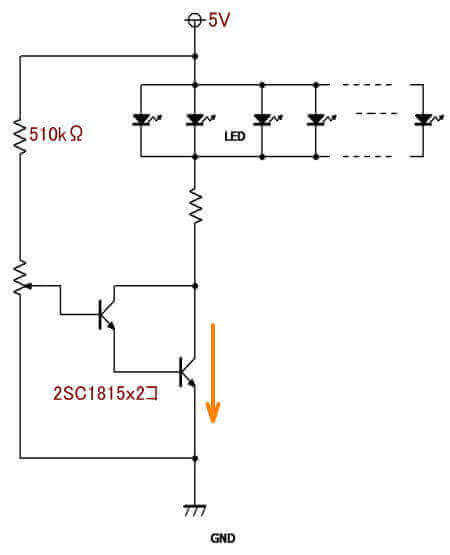
前のページのものを参考にして、このような回路で、ボリュームを回すと、LEDが暗くなる様子を見ようと思います。
先の実験では、510kΩを介して、ベース電流を7μA流すと70mA流れたので、LED1個に付き10mA流れるとすれば70/10=7個、5mA流れるとすれば14個くらいの数のLEDが点灯できそうです。
計算する数字としては、100mAの電流が流れることを前提にして考えていきます。
図のようにLEDを並列にすると、それぞれのLEDに加わる電圧は同じなので、LEDの特性が同じであれば、同じように光ってくれるはずですね。
LEDの電流制限抵抗・ベース電流用抵抗を計算してみます
LED点灯のために100mA流すとすると、LEDの順電圧を3.5Vとすると、R=E/I から、(5-3.5)/0.1=15Ω の電流制限抵抗を取り付けます。
抵抗器の大きさを考えると 電力W=IE=I2R=0.05Wで、1/2W形の抵抗器がほしいのですが、手持ちがないので、これについても、手元にある33Ω(1/8W)を2個並列にしたところ、16Ω(実測)でしたので、このようにして使います。
ここで今回は、非常に小さなベース電流を、ダーリントン接続回路で、10000倍に増幅するので、ボリュームの抵抗値について、少し考えないといけません。
ベース電流については、前回は100kΩのボリュームを使ったのですが、それでは、電圧降下用に使っている510kΩより小さい抵抗なので、7μAのほとんどがアース側に流れてしまって、ベースに電流が流れなくなるので、1桁大きい1MΩの可変抵抗器にします。
そうすると、 1.4/15000000=0.9μA がアースに流れる電流なので、ベースには (7-0.9)≒6μA が流れるはずで、増幅率が約10000倍とすると、6x10000=60mAの電流が流れる・・・と計算できます。
ここでは、LEDはとりあえず10個を並列につけてみます。
回路を組んで、店長させて、その時の電流値をも測ります。


点灯してみると、全電流が35mA程度しか流れていませんが、それでも、十分光ります。
このLEDはいろいろな色に変化して点滅する、かなり派手なLEDです。
YouTubeに点灯している様子をアップしました。(眩しい映像なので、凝視しないように注意ください)
映像では、最初は35mA程度で点灯し、途中から、2mA程度までボリュームを絞り、また、35mA に戻している映像になっています。
まだまだ電流的には余裕あるので、かなり多くのLEDが点灯できそうですね。
ただ、組み上がった状態で、ベース電流が1μAでコレクタ電流が39mA前後になっているので、単純な計算での増幅率は 39000倍 という数字になってしまいますし、ベース電流が2000μレンジで測って 0μA となっていても 15mA以上のコレクタ電流が流れています。
0では計算できないので、1μだとすると、15/0.001≒15000 となりますが、いずれにしても、これらの数字は、どう考えても正しいとは思えません。
1μAという小さな電流の数字は、簡単なテスターで測るのは無理だと考える以外の理由が思いつきませんが、ともかく 1つのトランジスタでは 100 程度の増幅率であるけれども、2つをダーリントン接続すると、200ではなく、10000倍というような、とてつもない大きな増幅率が得られることがわかりました。
*****
次は、電界効果トランジスタFETについて見ていきましょう。
Page Top▲
