理論や計算よりもまず工作してみて楽しみましょう
電気・電子の理論や計算が嫌いな人も、それらがわからないでも電子工作は楽しめますから、自分で楽しむ方法を見つけましょう。
このHPでは、難しい内容はありません。オームの法則、抵抗値の合成、電力など、中学時代に習ったものしか使っていません。
それらを知らなくてもOKで、音を出してみる、LEDをチカチカさせてみる … などの「やりたいこと」をやって、必要になったときに学びなおせばいいもので、初めから学ぶと嫌になってやる気がそがれるだけです。
私の場合も、HPの文章を書くので基本的な電気計算を知っておいたほうがいいだろうと思って、下の本を購入して、直流関係だけを一通り読んだのですが、交流理論は読んでいません。
もちろん、直流理論も当面は不要です。 このHPの内容は、メーカーのデータシートなどにある一般的なものをまねて使っていますので、少しそこから外れて何かをしようとするときに初めて、理論や計算が役に立ってくるだろうと、その時のために、自分が読めそうな1冊の本を購入しています。
 |
価格:2200円 |
それもあって、ここでは、このHPの回路図、オームの法則、合成抵抗などのほかに、知っておいたほうがいいと思うことを紹介するにとどめます。
切れている回路とつながっている回路の電圧はいくら?
この上側の図は、2つの電圧差のある回路をつなぐ際のプルアップやプルダウン抵抗などに関連するのですが、V1~V6の6か所の電圧はいくらですか? という問題の答えを考えてみてください。
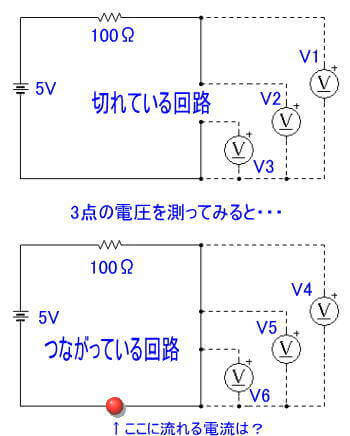
答えは、V1=V2=は5V で、それ以外は0Vです。 OKでしたか?
私は、V1とV2は電源と同じ5V ということを頭で理解できずに、回路を組んで電圧を測って納得したのですが、もしも 5V ではなく、100Vで抵抗が100kΩでは、V1とアースを手で握ると確実に感電します。
もちろん感電して死ぬことはありませんが。
ここで、抵抗器は、電圧を下げる役割と電流を下げる役割
私はこのことを知りませんでした。
回路中の抵抗器は、電圧を下げる役割と電流を制限する役割があって、上の「開いた回路」の抵抗器は電流を下げる役割、下側の「閉じた回路}では、電圧と電流を下げる役割をしているということです。
つまり、開いた回路では電源の電圧がかかっていても、抵抗器で電流が下げられています。
これがわかって、下のような道具を作ったところ、結構使い道があります。これは 「電圧調整器」です。

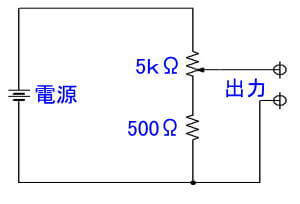
回路図では、こんな感じのもので、5Vの電源を使えば、ボリュームを回せば、0.5V~5Vの電圧が取り出せるという簡単な道具です。1/10~1/1の電圧が取り出せます。
低周波発振器の出力電圧を調整したり、常用の電源の5Vより低い電圧を使うために作ったのですが、オームの法則から、電流I=E/R=5/(5000+500)=1mA で、ボリューム最小では 5/500=10mAが流れるということがわかります。
もっと電流を流したいのなら、抵抗値の小さいもの似すればいいだけですね。
このように、「ちょっと何か変わったことをやってやろう・・・」というときに、オームの法則、抵抗の合成の考え方などは便利で、こういう道具を作ってみると、電圧や電流を変えるというイメージがわかってきますから、何かの参考に。
(参考)ここで使っている【回路図】について
このHPの回路図は、 フリーソフトBSch3V を使わせていただいて書いています。
「BSch3V」というフリーソフト(こちら)のサイトから無料ダウンロードできます。興味があれば使ってみてみてください。
この抵抗記号などの表記は最新のJIS表記ではないのですが、私自身もこの書き方のほうがわかりやすいので、そのまま使わせていただいています。
理論は必要になったら学べばいい・・・と書きましたが、オームの法則も、抵抗の合成も、電力の計算も中学校で習っているものですが、多分、忘れているでしょうから、思い出しながら以下を読み流していただくといいでしょう。
「オームの法則」について知っているとよいこと
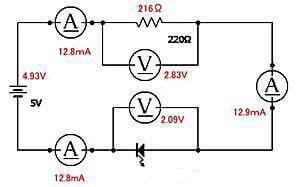
ちなみに、上の問題図の赤丸部分の電流値は、「オームの法則」を使って求められますし、簡単に測定することもできます。
私のオームの法則の覚え方は E=IR です。
赤丸部分の電流は、電圧=電流x抵抗 の式を 電流=電圧/抵抗 と変形すると、電源が5Vでは、抵抗100Ωに流れる電流は、 5/100=0.05A(=50mA) となります。(この50mAは小さな抵抗器では注意しないといけない電流値です。この後で取り上げています)
100V100kΩの場合は、100/100000=0.001A(=1mA)ですから、これらで感電して死ぬことはないということが計算するとわかります。 100Vを試すのは怖いですから、計算であらかじめわかるのは便利です。
このように、電圧・電流・抵抗のうちの2つがわかれば、残りの1つが計算できるのが「オームの法則」のいいところで、電子工作では、「オームの法則は常に正しい!」とする決まりがあります。
つまり、オームの法則は常に成り立っているとして、さらに、下のこともあわせて詮索しないことになっています。
1)テスターで測った電圧値や電流値は「正しい」
2)導線の抵抗は考えないし、抵抗の温度変化も考えない。
3)電源や抵抗器などの誤差は無視する。
これらの説明はながくなるので割愛しますが、「オームの法則はどこででも使うことができる」ということです。
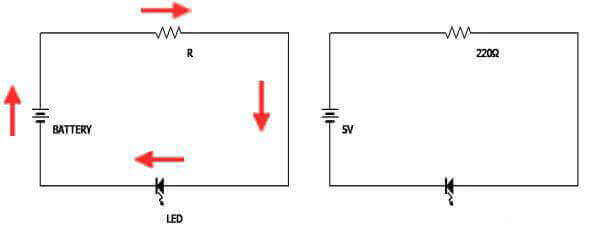
オームの法則には、2つの内容があって、「①導線の電流は両端の電位差に比例し、その比例定数は一定で、その逆数が抵抗である」「②導線の抵抗は長さに比例し、断面積に反比例する」があります。 このように文字で書くと難しそうですが、
第1法則は 「電流=電圧/抵抗」という内容で、第2法則はここでは特に覚えていなくてもいいとしておきます。
ここでは、電流はI、電圧はE、抵抗はRと表記していますが、I・E・Rではなく、A・V・R などと表示してもいいですし、E=IR I=E/R R=E/I でも、V=AR A=V/R R=V/A でも、V=IR でも、電圧=電流x抵抗 でもよいということで、私は E=IR だけを覚えていて、都度式を変形して使っています。
電力についてもよく使います
電力(W:ワット)=電圧(V:ボルト)x電流(A:アンペア) です。 この電力をたくさん消費すれば「熱」がたくさん発生するのですが、これが重要です。
熱は電流が流れることで発生するのですが、電流を流すためには電圧が必要なので、熱の大小は電力で考えるとイメージしやすいでしょう。
オームの法則の V=AR などから、 W=A2R=V2/R などに変形して計算することなどができますので、これを知っておくと危険対応ができて便利です。
市販の抵抗値は飛び飛び
 市販の抵抗器セット
市販の抵抗器セット
市販の抵抗器は飛び飛びの値のものしかありませんので、計算値に近い値の抵抗器を無理やり使うことがしばしば起こります。
趣味の電子工作では、オームの法則などで計算した抵抗値のものはまず市販されていませんので、ほとんどが、計算値に近い抵抗器を使います。
そうすると、計算した電流や電圧も変わりますが、趣味の電子工作はこれでOKという場合が多いのです。
このようなアバウトなものにも慣れていく必要があるということを覚えておいてください。
小さい抵抗器は熱くなりやすい
このHPで使う抵抗器のほとんどは、このような1/8W型(=0.125W)の小さな抵抗器ですので、5Vで25mA(0.025A)でもう目いっぱいです。 触れると抵抗器が熱くなっています。
抵抗器は容量の1/2~1/3以内の電力で使うのが推奨されますが、10mAまでしか使えないと実験がしにくいので、このHPでは小さな抵抗器でそれ以上の電流も短時間使用しています。 でも、この「電流と熱」は常時意識している必要があります。
抵抗器に触れて、熱くないかどうかを確かめるのですが、1/8Wの小さな抵抗器では常に意識していないと危険です。
市販の抵抗値がなければ合成するかアバウトで行くか
現実的には、計算して合成抵抗を使うことはほとんどありません。
直列での「足し算」は簡単ですので使うこともあるかもしれませんが、並列の割り算は大変ですので、同じオーム数で半分のオーム数にする以外は、私は適当な抵抗値で間に合わせて使いがちです。
もちろん、いずれの時も、「電流と熱」に注意することは忘れないようにしましょう。
1)直列
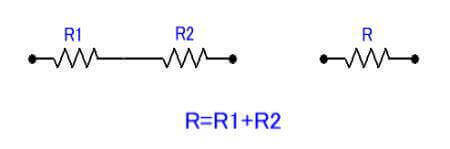
2)並列
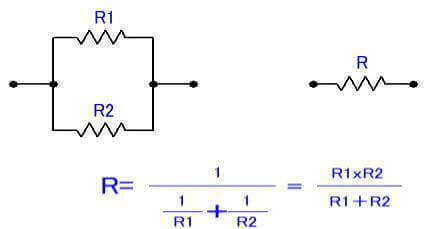
【プラスして覚えておくこと】 このとき、直列の場合は、回路に流れる電流が等しい、並列の場合は、各抵抗器に掛かる電圧が等しい という考え方を使うことがよく出てきます。 これは、出てきたときに説明していますが、覚えておくと便利です。
*********このように、少しの何かの理論や数式からいろいろ発展して考えていくのは楽しいと思えるようになればしめたものです。 いやいや覚えるのではなく、ともかく「楽しめる」電子工作であれば長続きするでしょう。ただ、危険は避けないといけません。

